Answer:
(a) 40 m
(b) 4 seconds
(c) 1 second, 45 m
(d) 1 second
Explanation:
The given height as a function of height is
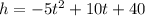
where t is the time in seconds and h is the height, in meters.
(a) At the starting time, t=0, the arrow is at the platform.
So, putting t=0, to get the height of the platform
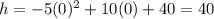 m
m
(b) For determining the length of time the arrow is in the air, first t determining the value of t for which h=0, we have
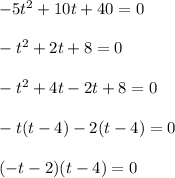
t=-2, t=4
Mathematically, the value of t for which the arrow is in the air is the time from -2 to 4 seconds.
But the arrow was at the platform at time t=0. So, neglecting the negative time, the time for which the arrow was in the air is the time from 0 to 4 seconds, i.e 4 seconds.
(c) Mathematically, the value of t for which the arrow is in the air is the time from t=-2 to t=4 seconds. So, in the middle of time, i.e at t=1 second the arrow will reach the maximum height.
Putting t=1 to get the maximum height, we have
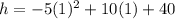
h=-5+10+40
h=45 m
Therefore, the maximum height is 45 m at t=1 second.
(d) Referinf option (c), at the time, t=1 second, the arrow has a height of exactly 45m above the ground