Answer:
The point is
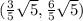
Explanation:
∵ The circle has center (0 , 0) and radius 3
∵ The equation of any circle is
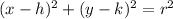
where (h , k) is the center of the circle and r is the radius of it
∴
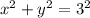
∴
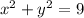
∵ The equation of the line is y = 2x
We will substitute y in the equation of the circle by 2x
∴
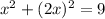
∴
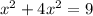
∴
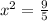
∴
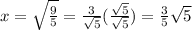
∴ y =
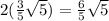
The line intersects the circle at point
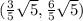
The decimal values (1.342 , 2.684)