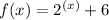Question

What is the inverse of the function of (x)=2^(x)+6

A. ^(-1)(x)=6+log_(2)x
B. f^(-1)(x)=log_(2)(x+6)
C. f^(-1)(x)=6log_(2)x
D. f^(-1)(x)=log_(2)(x-6)

Answer 1

Option D.

Explanation:

To find the inversion of a function follow the following procedure

1) Replace x with y in the function and clear y

`y=2^((x)) + 6` ------>
`x = 2^((y))+ 6`

`x-6 = 2^y`

`y = log_2(x-6)`

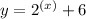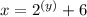
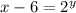
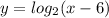
2) Check. The range of f(x) is the domain of
`f^(-1)(x)`.

So if f(a) = b, this means that
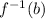`f^(-1)(b)` = a.

`f(2) = 2^2+ 6 = 10`

`f^(-1)(x) = log_2(10-6) = 2`

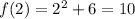
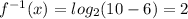
Is fulfilled. Therefore
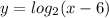`y=log_2(x-6)` is the inverse of
`f(x) = 2^((x)) +6`