Question

Numer 9 and 10. Need Solutions​

Answer 1

QUESTION 9

The given function has x-intercepts at;

`x=-2` with multiplicity 1.

`x=0` with multiplicity even, say 2.

`x=3` with multiplicity 1.

By the factor theorem;
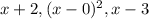`x+2,(x-0)^2,x-3` are factors of the polynomial function.

The possible formula for the graph is

`p(x)=ax^2(x+2)(x-3)`

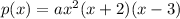
The point (-1,4) lies on this graph

`4=a(-1)^2(-1+2)(-1-3)`

`4=-4a`

`a=-1`

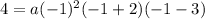
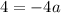
Hence a possible formula is

`p(x)=-x^2(x+2)(x-3)`

QUESTION 10

The given polynomial function has x-intercept at x=-2, with and odd multiplicity, say 1.

It was given that;

`p(i)=0`

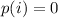
This implies that
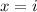`x=i` is a solution.

By the complex conjugate property,
`x=-i` is also a solution.

By the factor theorem;

`P(x)=a(x+2)(x-i)(x+i)`

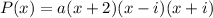
Apply difference of two squares and simplify to get;

`P(x)=a(x+2)(x^2+1)`

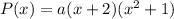
The graph passes through (2,-4).

`-4=a(2+2)(2^2+1)`

`-4=20a`

`a=-(1)/(5)`

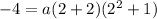
A possible formula is

`P(x)=-(1)/(5)(x+2)(x^2+1)`