Question

You have two rectangular prisms (Prism A and Prism B). Prism A has the following dimensions: length x, width y, and height z. Prism B is made by multiplying each dimension of Prism A by a factor of m, where m >0.

(a) Write a paragraph proof to show that the surface area of Prism B is 2 times the surface area of Prism A.

(b) Write a paragraph proof to show that the volume of Prism B is 3 times the volume of Prism A.

Answer 1

Part A) The surface area of prism B is equal to the surface area of prism A multiplied by the scale factor (m) squared

Part B) The Volume of prism B is equal to the Volume of prism A multiplied by the scale factor (m) elevated to the cube

Explanation:

Part A) we know that

The scale factor is equal to m

The surface area of the prism is equal to

`S=2B+Ph`

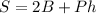
where

B is the area of the base

P is the perimeter of the base

h is the height of the prism

we have

Prism A

`B=xy\ units^(2)`

`P=2(x+y)\ units`

`h=z\ units`

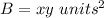
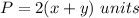
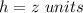
substitute

`SA=[2(xy)+2(x+y)z]\ units^(2)`

Prism B

`B=(mx)(my)=(xy)m^(2)\ units^(2)`

`P=2(mx+my)=2m(x+y)\ units`

`h=mz\ units`

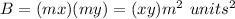
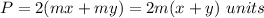
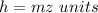
substitute

`SB=[2(xym^(2))+2m(x+y)mz]\ units^(2)`

`SB=[2(xym^(2))+2m^(2)(x+y)z]\ units^(2)`

`SB=m^(2)[2(xy)+2(x+y)z]\ units^(2)`

therefore

The surface area of prism B is equal to the surface area of prism A multiplied by the scale factor (m) squared

Part B) we know that

The volume of the prism is equal to

`V=Bh`

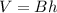
where

B is the area of the base

h is the height of the prism

we have

Prism A

`B=xy\ units^(2)`

`h=z\ units`

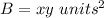
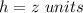
substitute

`VA=[(xyz]\ units^(3)`

Prism B

`B=(mx)(my)=(xy)m^(2)\ units^(2)`

`h=mz\ units`

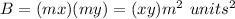
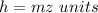
substitute

`VB=[(xym^(2))mz]\ units^(3)`

`VB=[(xyzm^(3))]\ units^(3)`

therefore

The Volume of prism B is equal to the Volume of prism A multiplied by the scale factor (m) elevated to the cube