Answer:
Part A) The surface area of prism B is equal to the surface area of prism A multiplied by the scale factor (m) squared
Part B) The Volume of prism B is equal to the Volume of prism A multiplied by the scale factor (m) elevated to the cube
Explanation:
Part A) we know that
The scale factor is equal to m
The surface area of the prism is equal to
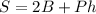
where
B is the area of the base
P is the perimeter of the base
h is the height of the prism
we have
Prism A
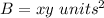
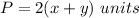
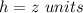
substitute
![SA=[2(xy)+2(x+y)z]\ units^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/cm9dvijhgtkfwgmw769zpcdpof06j4d0y0.png)
Prism B
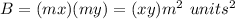

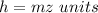
substitute
![SB=[2(xym^(2))+2m(x+y)mz]\ units^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/rggpl932sig871vn8il4e3xguut3n74xax.png)
![SB=[2(xym^(2))+2m^(2)(x+y)z]\ units^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/h5vzeg1toj67jtrfdel0dzhht01dp7zjz4.png)
![SB=m^(2)[2(xy)+2(x+y)z]\ units^(2)](https://img.qammunity.org/2020/formulas/mathematics/high-school/srre4lxst8670mhkj6kgxwn7tmk7a6e1c5.png)
therefore
The surface area of prism B is equal to the surface area of prism A multiplied by the scale factor (m) squared
Part B) we know that
The volume of the prism is equal to

where
B is the area of the base
h is the height of the prism
we have
Prism A
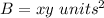
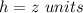
substitute
![VA=[(xyz]\ units^(3)](https://img.qammunity.org/2020/formulas/mathematics/high-school/o1pihv75c0j0x4d6s03anwsol8gbfgv80e.png)
Prism B
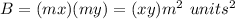
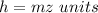
substitute
![VB=[(xym^(2))mz]\ units^(3)](https://img.qammunity.org/2020/formulas/mathematics/high-school/nj5usfvoee9vby0ixkzrpy4yla9oixwagx.png)
![VB=[(xyzm^(3))]\ units^(3)](https://img.qammunity.org/2020/formulas/mathematics/high-school/2ocjk7n28jq49xagrr15lf11vxbeyttgcb.png)
therefore
The Volume of prism B is equal to the Volume of prism A multiplied by the scale factor (m) elevated to the cube