Answer:
Hence, the number of daylilies in the first year were:
600
Explanation:
It is given that:
the recursive formula
 represents the number of daylilies, a, after n years.
represents the number of daylilies, a, after n years.
Also we are given that in the fifth year they have 2,225 daylilies.
i.e.
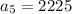
Also,
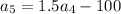
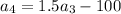
This means that:
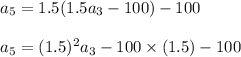
Similarly,
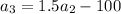
so,
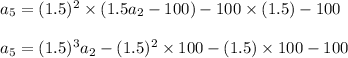
and so, putting
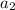 in terms of
in terms of
 we get:
we get:
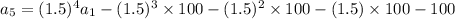
Now on putting the value of
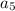 we find the value of
we find the value of


Hence, the number of daylilies in the first year were:
600