Answer:
Approximately 3 grams left.
Explanation:
We will utilize the standard form of an exponential function, given by:
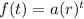
In the case of half-life, our rate r will be 1/2. This is because 1/2 or 50% will be left after t half-lives.
Our initial amount a is 185 grams.
So, by substitution, we have:
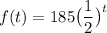
Where f(t) denotes the amount of grams left after t half-lives.
We want to find the amount left after 6 half-lives. Therefore, t = 6. Then using our function, we acquire:
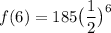
Evaluate:
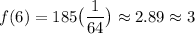
So, after six half-lives, there will be approximately 3 grams left.