Answer:
(-3, 2).
Explanation:
ABCD is a parallelogram. Consider the two vectors:
The length of BA and CD are the same since the two are on opposite sides of the parallelogram. They are parallel to each other and point in the same direction. As a result, vector BA = vector CD.
The position vector of each vertice is the same in value as the coordinate of that point. For example, the coordinate of point A is (8, 2).
 .
.
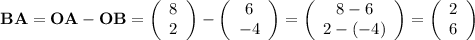 .
.
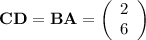 .
.
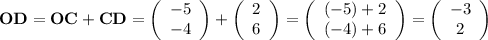 .
.
The same rule goes the other way:
 .
.
Coordinates of point D: (-3, 2).