Answer:
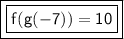
Explanation:
We are asked to find f(g(-7)) given these 2 functions:
We must work from the inside out, so first find g(-7).
1. g(-7)
The function for g is:
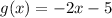
Since we want to find g(-7), plug -7 in for x.
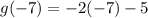
Solve according the PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.
Multiply -2 and -7.
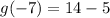
Subtract 5 from 14.

2. f(9)
Refer back to the original problem: f(g(-7))
Since we found that g(-7) is 9, we can substitute 9 in: f(9)
The function for f is:

Plug 9 in for x.
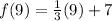
Solve according to PEMDAS and multiply 1/3 and 9.
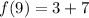
Add 3 and 7.
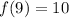
f(g(-7) is equal to 10