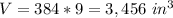Answer:
Part A) The scale factor is

Part B)The volume of the prism made by ∆PQR is
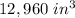
Part C) The volume of the prism made by ∆XYZ is
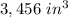
Explanation:
we know that
If two figures are similar, then the ratio of its corresponding sides is equal and this ratio is called the scale factor
In this problem triangles PQR and XYZ are similar
because

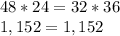
Part A) What is the scale factor from ∆PQR to ∆XYZ?
The scale factor is equal to
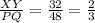
The scale factor is less than 1
therefore
Is a reduction
Part B) Suppose the height of the prism made by ∆PQR is 15 inches. What is the volume of the prism made by ∆PQR?
we know that
The volume of the triangular prism is equal to

where
B is the area of the base of the prism ( area of triangle ∆PQR)
h is the height of the prism
Find the area of the base B
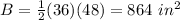
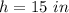
substitute the values
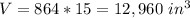
Part C) Suppose the volume of the prism made by ∆PQR is 7776 〖"in" 〗^3. What is the volume of the prism made by ∆XYZ?
step 1
Find the height of the prism made by ∆PQR
The volume of the triangular prism is equal to

solve for h
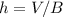
we have
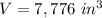
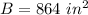
substitute in the formula
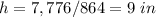
step 2
Find the volume of the prism made by ∆XYZ
The volume of the triangular prism is equal to

Find the area of the base B ∆XYZ
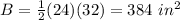
 -------> see step 1
-------> see step 1
substitute the values