Question

Cassidy's diving platform is 6 ft above the water. One of her dives can

be modelled by the equation d = x2 - 7x + 6, where d is her position
relative to the surface of the water and x is her horizontal distance from
the platform. Both distances are measured in feet. How deep did Cassidy
go before coming back up to the surface?

Answer 1

Before coming back up to the surface the maximum depth, Cassidy went was 6.25 ft. below the water surface

Explanation:

The height of Cassidy's diving platform above the water = 6 ft.

The equation that models her dive is d = x² - 7·x + 6

Where;

d = Her vertical position or distance from the water surface

x = Here horizontal distance from the platform

At Cassidy's maximum depth, we have;

dd/dx = d(x² - 7·x + 6)/dx = 2·x - 7 = 0

x = 7/2 = 3.5

∴ At Cassidy's maximum depth, x = 3.5 ft.

The maximum depth,
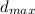`d_(max)` = d(3.5) = 3.5² - 7 × 3.5 + 6 = -6.25

The maximum depth, Cassidy went before coming back up to the surface =
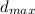`d_(max)` = -6.25 ft = 6.25 ft. below the surface of the water.