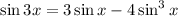Question

Trignometry problem help plz
no 3, 5 and 6​

Answer 1

3. First factor
`\cos^6A-\sin^6A` as a difference of cubes:

`\cos^6A-\sin^6A=\underbrace{(\cos^2A-\sin^2A)}_(\cos2A)(\cos^4A+\cos^2A\sin^2A+\sin^4A)`

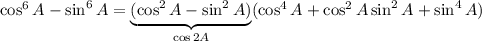
For the remaining group, apply the double angle identity.

`\cos^2A=\frac{1+\cos2A}2`

`\sin^2A=\frac{1-\cos2A}2`

`\implies\begin{cases}\cos^4A=\left(\frac{1+\cos2A}2\right)^2=\frac{1+2\cos2A+\cos^22A}4\\\\\cos^2A\sin^2A=\frac{(1+\cos2A)(1-\cos2A)}4=\frac{1-\cos^22A}4\\\\\sin^4A=\left(\frac{1-\cos2A}2\right)^2=\frac{1-2\cos2A+\cos^22A}4\end{cases}`

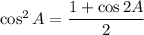
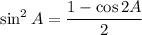
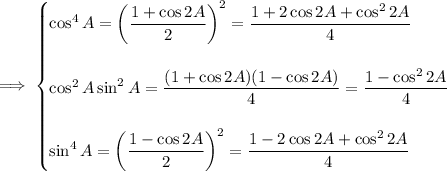
`\implies4(\cos^6A-\sin^6A)=\cos2A[(1+2\cos2A+\cos^22A)+(1-\cos^22A)+(1-2\cos2A+\cos^22A)]`

`=\cos2A(3+\cos^22A)=\cos^32A+3\cos2A`

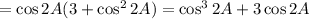
5. seems rather tricky. You might want to post another question for that problem alone...

6. Factorize the left side as a sum of cubes:

`\cos^320^\circ+\sin^310^\circ=(\cos20^\circ+\sin10^\circ)(\cos^220^\circ-\cos20^\circ\sin10^\circ+\sin^210^\circ)`

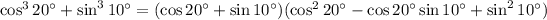
From here we have to prove that

`\cos^220^\circ-\cos20^\circ\sin10^\circ+\sin^210^\circ=\frac34`

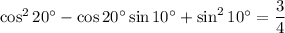
We can write everything in terms of sine:

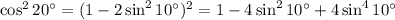`\cos^220^\circ=(1-2\sin^210^\circ)^2=1-4\sin^210^\circ+4\sin^410^\circ` (double angle identity)

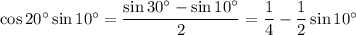`\cos20^\circ\sin10^\circ=\frac{\sin30^\circ-\sin10^\circ}2=\frac14-\frac12\sin10^\circ` (angle sum identity)

After some simplifying, we're left with showing that

`4\sin^410^\circ-3\sin^210^\circ+\frac12\sin10^\circ=0`

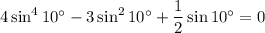
or

`4\sin^310^\circ-3\sin10^\circ+\frac12=0`

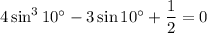
This last equality follows from what you could the triple angle identity for sine,

`\sin3x=3\sin x-4\sin^3x`