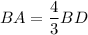Question

Given: △ABC, D∈

AC
m∠BDC=m∠ABC
AD=7, DC=9
Find: BC, BD BA

Answer 1

BC = 12, BD:BA = 3/4

Explanation:

Previous answers for the first half of the problem were correct

for the ratio aspect of the question, however...

don't cross multiply; instead just reciprocate the fraction so that instead of getting BA:BD you have BD:BA

so:

BA:BD = 4:3

but

BD:BA = 3:4

hope this helps!

Answer 2

`\large\boxed{BC=12,\ BA=(4)/(3)BD}`

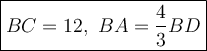
Explanation:

Look at the picture.

ΔABC and ΔBDC are similar (AA - If two triangles have two of their angles equal, the triangles are similar).

Therefore the sides are in proportion:

`(AC)/(BC)=(BC)/(DC)`

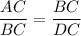
We have:

AC = 16

BC = x

DC = 9

Substitute:

`(16)/(x)=(x)/(9)` cross multiply

`x^2=(16)(9)\to x=√((16)(9))\\\\x=√(16)\cdot\sqrt9\\\\x=4\cdot3\\\\x=12`

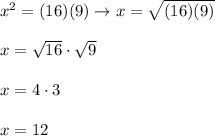
Therefore BC = 12.

Calculate the similarity scale:

`k=(AC)/(BC)\to k=(16)/(12)=(16:4)/(12:4)=(4)/(3)`

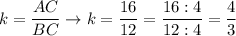
Therefore we have the poportion:

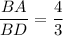`(BA)/(BD)=(4)/(3)` cross multiply

`3BA=4BD` divide both sides by 3

`BA=(4)/(3)BD`