Question

Jack bought a new car in 2014 for 28,000. If the value of the car decreases by 14% each year, write an exponential model for the value of the car. Then estimate the year the car will have a value of 5,000

Answer 1

Answer: 1)
`28000(0.86)^x`

2) After 11.422 years( approx ) since 2014 the value of car will be 5000.

Explanation:

Since, the initial value of the car = 28000

The yearly decrease in the value of car = 14 %

Hence, the value of car after x years

=
`28000(1-(14)/(100))^x`

=
`28000(1-0.14)^x`

=
`28000(0.86)^x`

Which is the required exponential function that shows the value of car.

Now let after t years, the value of car is 5000,

`\implies 28000(0.86)^y=5000`

`\implies 28(0.86)^y=5`

`\implies (0.86)^y = 0.178571429`

By taking log both sides,

`\implies y log(0.86)=log(0.178571429)`

`\implies y=11.4224479\approx 11.422\text{ years}`

Answer 2

In 2026 car will have a value of $5,000.

Explanation:

We have been given that Jack bought a new car in 2014 for 28,000. If the value of the car decreases by 14% each year.

Since we know that an exponential function is in form:
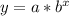`y=a*b^x`, where,

a = Initial value,

b = For decay or decrease b is in form (1-r), where r represents decay rate in decimal form.

Let us convert our given decay rate in decimal form.

`14\%=(14)/(100)=0.14`

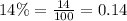
Upon substituting a =28,000 and r=0.14 in exponential decay function we will get,

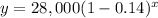`y=28,000(1-0.14)^x`, where x represents number of years after 2014.

Therefore, the function
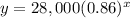`y=28,000(0.86)^x` represents the value of car x years after 2014.

To find the number of years it will take to car have the value of $5,000, we will substitute y=5,000 in our function.

`5,000=28,000(0.86)^x`

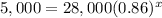
Let us divide both sides of our equation by 28,000.

`(5,000)/(28,000)=(28,000(0.86)^x)/(28,000)`

`0.1785714285714286=(0.86)^x`

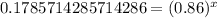
Let us take natural log of both sides of our equation.

`ln(0.1785714285714286)=ln((0.86)^x)`

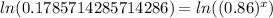
Using natural log property
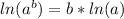`ln(a^b)=b*ln(a)` we will get,

`ln(0.1785714285714286)=x*ln(0.86)`

`(ln(0.1785714285714286))/(ln(0.86))=(x*ln(0.86))/(ln(0.86))`

`(-1.7227665977411033893)/(-0.1508228897345836)=x`

`x=11.422447\approx 12`

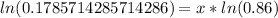
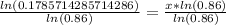
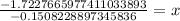
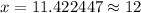
As in the 12th year after 2014 car will have a value of $5,000, so we will add 12 to 2014 to find the year.

`2014+12=2026`

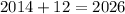
Therefore, in 2026 car will have a value of $5,000.