Answer: The streets are 225 feet apart.
Explanation:
Since we have given that
Length of frontage on one street = 500 feet
Length of frontage on other street = 300 feet
Area of this figure = 90000 sq. feet
Let the distance between the street be 'h'.
Since it forms trapezium:
So, Area of trapezium would be
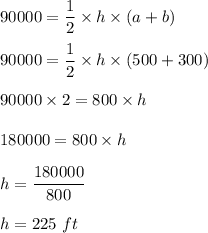
Hence, the streets are 225 feet apart.