Answer:
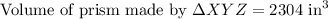
Explanation:
Let us assume that both prisms are similar, so we can use proportions to solve for the volume of prism made by triangle XYZ.
Let us find the proportion between the sides of both triangles.
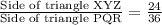

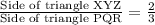
Since for volume of triangular prism we multiply base area and height of the prism, this means we will have to multiply the proportion of each side length 3 times to find the proportion of volumes between our both prism.
So we can set proportion for volume of both prisms as:
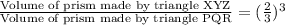
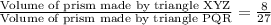
Upon substituting volume of prism made by triangle PQR we will get,
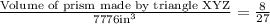
Let us multiply both sides of our equation by 7776 cubic inches.
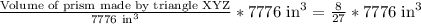
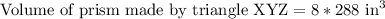
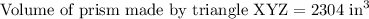
Therefore, the volume of prism made by triangle XYZ is 2304 cubic inches.