Question

A solid sphere of radius r carries charge q distributed uniformly throughout its volume. find the potential difference from the sphere's surface to its center.

Answer 1

Answer: The potential difference from the sphere's surface to its center is zero.

Step-by-step explanation:

The expression for the potential difference due to charge is as follows;

`\Delta V=(q)/(4\pi \epsilon _(0)r)`

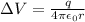
Here,
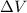`\Delta V` is the potential difference, q is the charge, r is the position and
`\epsilon _(0)}` is the absolute permittivity of free space.

In the given problem, a solid sphere of radius r carries charge q distributed uniformly throughout its volume.

To find the potential difference from the sphere's surface to its center. Put r=0 in the expression of the potential difference.

`\Delta V=(q)/(4\pi \epsilon _(0)(0))`

`\Delta V=0`

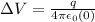
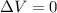
Therefore, the potential difference from the sphere's surface to its center is zero.