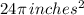Answer:
The exact area of the sector in terms of π is
Explanation:
Given the radius of circle 12-inch and the central angle measure of 60°.
We have to find the the exact area of the sector in terms of π.
As the area of sector can be calculated by the formula
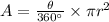
where
 is the central angle in degree and r is the radius of circle.
is the central angle in degree and r is the radius of circle.
Now,
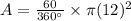
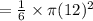

Hence, the exact area of the sector in terms of π is