Answer:
Horizontal compression by a factor of 3.
Reflection over the x-axis.
Explanation:
The parent function is
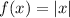
The transformed function is
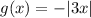
Notice that the transformation involves to multiply the function with -1 and multiply the independent variable by 3.
Remember, if we multiple the independent variable by a number greater than 1, then the function will compress horizontally, that is, in the direction of x-axis.
Additionally, if we multiply the function by a negative number as -1, the function graph will reflect across the x-axis.
The image attached shows these transfomations.
Therefore, the right answers are:
- Horizontal compression by a factor of 3.
- Reflection over the x-axis.