Question

This graph shows the solution to which inequality?

Answer 1

The graph shows the solution of the inequality y >
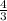`(4)/(3)` x - 2 ⇒ D

Explanation:

In the inequality,

• If the sign of inequality is ≤ or ≥, then the line that represents it must be a solid line

• If the sign of inequality is < or >, then the line that represents it must be a dashed line

• If the sign of inequality is > or ≥, then the shaded area must be over the line

• If the sign of inequality is < or ≤, then the shaded area must be under the line

From the given graph

∵ The slope of the line =
`(2--6)/(3--3)` =
`(2+6)/(3+3)` =
`(8)/(6)` =
`(4)/(3)`

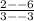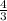
∵ The y-intercept is (0, -2)

∵ The line is dashed and the shaded area is over the line

→ By using the 2nd and 3rd notes above, the line is dashed and

the sign of inequality is >

∴ The inequality is y >
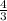`(4)/(3)` x - 2

∴ The graph shows the solution of the inequality y >
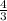`(4)/(3)` x - 2