Question

The equation of a circle is (x - 4)2 + (y + 3)2 = 36. Where is (2, -1) located in relation to the circle?

On the circle

In the interior of the circle

In the exterior of the circle

At the center of the circle

Answer 1

In the interior because if you plug in the point it is less than 36 and it is not the center of the circle

Answer 2

For this case we have that the center of the circle is given by the point (4, -3). The radius is
`r = 6`

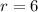
We find the distance between the center of the circle and the given point by means of the following formula:

`d = \sqrt {(x_ {2} -x_ {1}) ^ 2+ (y_ {2} -y_ {1}) ^ 2}`

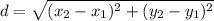
Let:

`(x_ {1}, y_ {1}) = (2, -1)\\(x_ {2}, y_ {2}) = (4, -3)`

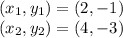
Substituting:

`d = \sqrt {(4-2) ^ 2 + (- 3 - (- 1)) ^ 2}\\d = \sqrt {(2) ^ 2 + (- 3 + 1) ^ 2}\\d = \sqrt {(2) ^ 2 + (- 2) ^ 2}\\d = \sqrt {4 + 4}\\d = \sqrt {8}\\d = 2.828427125`

The diatnce between the center and the given point is less than the radius of the circle, therefore, the point is inside.

Answer:

Option B