For this case we have that the center of the circle is given by the point (4, -3). The radius is
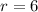
We find the distance between the center of the circle and the given point by means of the following formula:
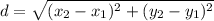
Let:
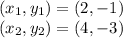
Substituting:
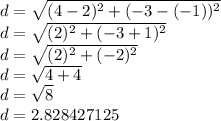
The diatnce between the center and the given point is less than the radius of the circle, therefore, the point is inside.
Answer:
Option B