Answer:
a) The translational kinetic energy of the particle at point A is 17.28 joules.
b) The speed of the particle at point B is approximately 5.270 meters per second.
c) The total work done on the particle as it moves from A to B is - 9.78 joules.
Step-by-step explanation:
Let be this particle a conservative system, that is, that non-conservative forces (i.e. friction, viscosity) are negligible.
a) The translational kinetic energy of the particle (
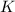 ), measured in joules, is determined by the following formula:
), measured in joules, is determined by the following formula:
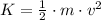 (1)
(1)
Where:
 - Mass, measured in kilograms.
- Mass, measured in kilograms.
 - Speed, measured in meters per second.
- Speed, measured in meters per second.
If we know that
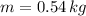 and
and
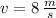 , the translational kinetic energy at point A is:
, the translational kinetic energy at point A is:
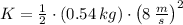

The translational kinetic energy of the particle at point A is 17.28 joules.
b) The speed of the particle is clear in (1):

If we know that
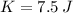 and
and
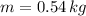 , then the speed of the particle at point B:
, then the speed of the particle at point B:
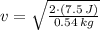
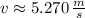
The speed of the particle at point B is approximately 5.270 meters per second.
c) According to the Work-Energy Theorem, the total work done on the particle as it moves from A to B (
 ), measured in joules, is equal to the change in the translational kinetic energy of the particle. That is:
), measured in joules, is equal to the change in the translational kinetic energy of the particle. That is:
 (2)
(2)
If we know that
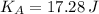 and
and
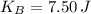 , then the change in the translational kinetic energy of the particle is:
, then the change in the translational kinetic energy of the particle is:
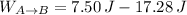
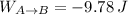
The total work done on the particle as it moves from A to B is - 9.78 joules.