Question

Given: △CDE m∠D=90°, DK ⊥ CE CD:DE=3:5, KE=CK+8 Find: CE

Answer 1

CE = 17

Explanation:

Lets assume :

CK=x

KE=x+8

CE= 2x+8

CD= y

DE=5/3y

We can then use the thereom of altitudes to hypotnuse and geometric means to get the system of equation:

y= √(x)(2x+8)

5/3 y= √(2x+8)(x+8)

So the equation would be:

(5/3*(√2x^2+8x))^2= (√2x^2+24x+64)^2

25/9*(2x^2+8x)= 2x^2+24x+64

9(50/9x^2 +200/9x) =9(2x^2+24x+64)

50x^2+200x=18x^2+216x+576

32x^2-16x-576=0

16[2x^2-x-36]=0

x=-4; x=9/2

CE=2x+8

CE=2(9/2)+8=17

Answer 2

The length of CE=17

Explanation:

In △CDE, m∠D=90°, DK ⊥ CE CD:DE=3:5, KE=CK+8

Let length of CK be y

KE=CK+8 = y+8

CE=2y+8

Please see the attachment for figure.

In ΔCDK and ΔDEK

∠CKD=∠DKE (each 90°)

∠CDK=∠DEK (opposite angle of right angle triangle)

∴ ΔCDK ≈ ΔDEK by AA similarity

`(CD)/(DE)=(CK)/(DK)`

`(3)/(5)=(y)/(√(9x^2-y^2))`

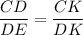
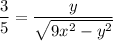
Squaring both sides

`(9)/(25)=(y^2)/(9x^2-y^2)`

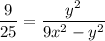
Cross multiply and get rid of denominator

`81x^2-9y^2=25y^2`

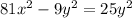
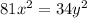`81x^2=34y^2`-------------(1)

In ΔCDK , Using Pythagorean theorem

`CD^2+DE^2=CE^2`

`9x^2+25x^2=(2y+8)^2`

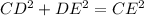
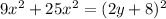
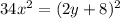`34x^2=(2y+8)^2`-------------(2)

Divide eq(1) and eq(2)

`(81)/(34)=(34y^2)/((2y+8)^2)`

`81(4y^2+32y+64)=1156y^2`

`324y^2+2592y+5184=1156y^2`

`832y^2-2592y-5184=0`

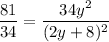
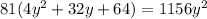
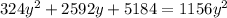
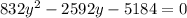
Using quadratic formula solve for y and we get

`y=4.5`

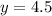
CE=2y+8 = 2(4.5) + 8 = 17

Hence, The length of CE=17