Answer:
The length of CE=17
Explanation:
In △CDE, m∠D=90°, DK ⊥ CE CD:DE=3:5, KE=CK+8
Let length of CK be y
KE=CK+8 = y+8
CE=2y+8
Please see the attachment for figure.
In ΔCDK and ΔDEK
∠CKD=∠DKE (each 90°)
∠CDK=∠DEK (opposite angle of right angle triangle)
∴ ΔCDK ≈ ΔDEK by AA similarity
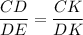
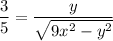
Squaring both sides
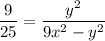
Cross multiply and get rid of denominator
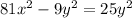
 -------------(1)
-------------(1)
In ΔCDK , Using Pythagorean theorem
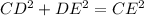
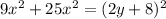
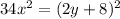 -------------(2)
-------------(2)
Divide eq(1) and eq(2)
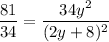
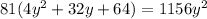
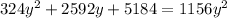
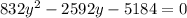
Using quadratic formula solve for y and we get
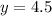
CE=2y+8 = 2(4.5) + 8 = 17
Hence, The length of CE=17