Question

Somebody please help me‍♀️

Answer 1

Result: 20

The result is rational because it can be written at the ratio of two integer's and it's decimal expansion does terminate or repeat​

Step-by-step explanation:

2√16 + 4√9

Calculate the square root of 16 and get 4.

2 × 4 + 4√9

Multiply 2 and 4 to get 8.

8 + 4√9

Calculate the square root of 9 and get 3.

8 + 4 × 3

Multiply 4 and 3 to get 12.

8 + 12

Add 8 and 12 to get 20.

20

Answer 2

Result:
`\boldsymbol{20}`

The result is rational because it can be written as the ratio of two integers and its decimal expansion does terminate or repeat.

=============================================

Step-by-step explanation:

Let's simplify the expression to get...

`2√(16)+4√(9)\\\\2√(4^2)+4√(3^2)\\\\2*4+4*3\\\\8+12\\\\20\\\\`

Therefore,
`2√(16)+4√(9)=20\\\\`

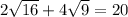
Since
`20 = (20)/(1)`, we have a rational number here. It's a fraction of two integers

`\text{rational number} = \frac{\text{integer}}{\text{integer}}`

We cannot have zero in the denominator.

One property of rational numbers is that the decimal expansion either terminates or it repeats (one option only).

In this case, we have a terminating decimal because 20 = 20.0; ie the decimal doesn't go on forever.

In contrast, something like 1/3 = 0.33333... has the '3's go on forever to be a repeating decimal.