Answer:
The polygon has 12 sides (a dodecagon).
Explanation:
Angles in a Regular Polygon
A polygon with n sides has a total sum of internal angles equal to 180°(n-2). This means that each angle (in a regular polygon) measures
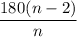
We are given the interior angle of 150°, thus:

Multiplying by n:

Operating

Rearranging and simplifying:

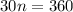

n = 12
The polygon has 12 sides (a dodecagon).