Answer:
option (d) is correct.
The mid points of the line segment whose ends points are (-2,-2) and (4,6) is (1,2)
Explanation:
Given: end points of a line segment as (-2,-2) and (4,6)
We have to find the mid points of the line segment whose ends points are given.
Mid point formula is stated as ,
For a line having end points as
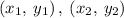 , the mid point can be calculated as,
, the mid point can be calculated as,
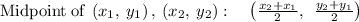
Here,
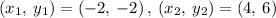
Substitute in mid point formula, we get,
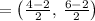
Solving further , we get,
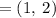
Thus, the mid points of the line segment whose ends points are (-2,-2) and (4,6) is (1,2)
Thus, option (d) is correct.