Hello!
The answer is: The transitive property.
Why?
Inequalities express the relative size between two values/numbers.
The transitive property of inequalities states that there's a way to relate two or more inequalities when they have at least a common value, and we can use it to create a relationship with a third or more values/variables.
For your statement, we have
A common value which is 5
Two inequalities expressing a relative size between two variables and a common value which is 5:
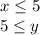
So, the inequalities are telling us that the common value (5) is higher or equal than x
and, the variable y is higher or equal than 5
So, using the transitive property we can safely assume that, y is higher or equal, than x
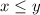
Have a nice day!