In the diagram below de and ef are tangent to o what is the measure of E

Question

asked Feb 14, 2020 224k views

2 Answers

Drom · Answer 1 · 2020-02-20T07:08:57+0000

Answer:

Option D is correct

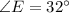
$\angle E = 32^(\circ)$

Explanation:

In the given diagram below DE and EF are tangent to O.

Join the point D and O and O and F as shown below.

It is given that:

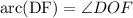
$\text{arc(DF)} = \angle DOF$

⇒
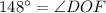
$148^(\circ) = \angle DOF$

or

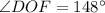
$\angle DOF = 148^(\circ)$

A line is tangent to circle if and only if the line is perpendicular to the radius drawn to the point of tangency.

Since, DE and EF are tangent

then:

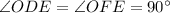
$\angle ODE = \angle OFE = 90^(\circ)$

In a quadrilateral EDOF:

Sum of all the angles add up to 360 degree.

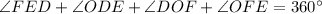
$\angle FED +\angle ODE + \angle DOF+ \angle OFE = 360^(\circ)$

Substitute the given values we have;

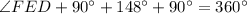
$\angle FED +90^(\circ)+ 148^(\circ) +90^(\circ) = 360^(\circ)$

⇒
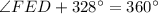
$\angle FED + 328^(\circ) = 360^(\circ)$

Subtract 328 degree from both sides we have;

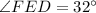
$\angle FED = 32^(\circ)$

Therefore, the measure of angle E is, 32 degree.