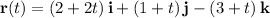Take the given vector by itself,
 . Scaling the vector by a scalar
. Scaling the vector by a scalar
 will stretch the vector. Any real number can take the place of
will stretch the vector. Any real number can take the place of
 ; when we consider all possible choices, we see that
; when we consider all possible choices, we see that
 traces out an infinite line through the origin and the point (2, 1, -1). (Left)
traces out an infinite line through the origin and the point (2, 1, -1). (Left)
Next, treat point P(2, 1, -3) as a vector,
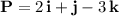 . (Upper right) By adding
. (Upper right) By adding
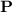 to
to
 , we get a new vector that, as we change the value of
, we get a new vector that, as we change the value of
 , traces out the line through point P which also happens to be parallel to
, traces out the line through point P which also happens to be parallel to
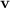 . (Lower right)
. (Lower right)
So the equation of this line in parametric form is
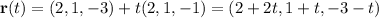
or in ijk notation,