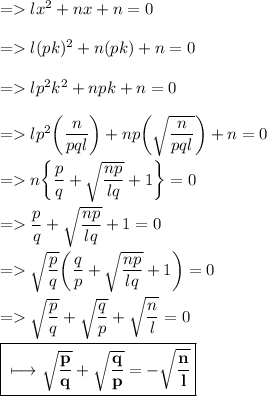Explanation:
Let the given ratio be pk : qk .
So , here the quadratic equation is lx² + nx + n = 0. With respect to Standard form ax² + bx + c = 0.
We have ,
→ Sum of roots = -b/a = -n/l = qk + pk
→ Product of roots = c/a = n/l = k²pq .
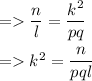
And here pk and qk is a root of the quadratic equation ,