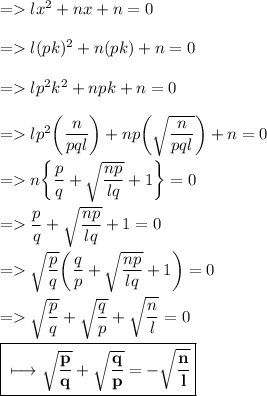Question

If the roots of the equation
lx²+nx+n=o is in the ratio p:q
then
√(p/q) + √(q/p)=?​

Answer 1

Explanation:

Let the given ratio be pk : qk .

So , here the quadratic equation is lx² + nx + n = 0. With respect to Standard form ax² + bx + c = 0.

We have ,

• a = l
• b = n
• c = n

→ Sum of roots = -b/a = -n/l = qk + pk

→ Product of roots = c/a = n/l = k²pq .

`=> (n)/(l) = (k^2)/(pq) \\\\=> k^2 =(n)/(pql)`

And here pk and qk is a root of the quadratic equation ,

`=> lx^2 + nx + n = 0 \\\\=> l(pk)^2 + n(pk) + n = 0\\\\=> lp^2k^2+npk + n = 0 \\\\=> lp^2\bigg( (n)/(pql) \bigg) + np\bigg(\sqrt{(n)/(pql)} \bigg) + n = 0 \\\\ => n\bigg\{(p)/(q)+\sqrt{(np)/(lq)}+1\bigg\} = 0 \\\\=> (p)/(q)+\sqrt{(np)/(lq)}+1 =0\\\\=>\sqrt{(p)/(q)} \bigg( (q)/(p)+\sqrt{(np)/(lq)}+1\bigg) = 0 \\\\=> \sqrt{(p)/(q)}+ \sqrt{(q)/(p)}+ \sqrt{(n)/(l)}=0 \\\\\boxed{\red{\bf\longmapsto \sqrt{(p)/(q)}+ \sqrt{(q)/(p)} = - \sqrt{(n)/(l)}}}`