Question

A power function with form y = ax passes through the points (2,

5
and 3,
81
Find the constants a
and pa=
p=

Answer 1

Answer: a = 47.3;

p = 0.65

Explanation: A power function is of the form
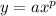`y=ax^(p)` and passes through points (2,5) and (3,81), i.e.:

`5=a.2^(p)`

`81=a.3^(p)`

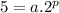
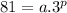
To determine the two unknows, solve the system of equations:

`log5=log(a.2^(p))`

`log81=log(a.3^(p))`

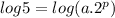
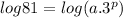
Using multiplication and power rules:

`log5=loga+plog2`

`log81=loga+plog3`

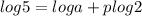
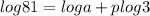
Giving values to constants:

0.7=loga+0.3p

2=loga+0.5p

This system of equations can be solved by subtracting each other:

`-1.3=-0.2p`

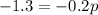
p = 0.65

Substituting p into one of the equations above:

`loga+0.5(0.65)=2`

`loga=1.675`

`a=10^(1.675)`

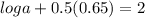
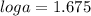
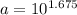
a = 47.3

The constants a and p of the power function which passes through points (2,5) and (3,81) are 47.3 and 0.65, respectively.