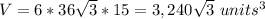Answer:
The volume of the hexagon is equal to
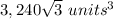
Explanation:
we know that
The volume of the prism is equal to
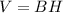
where
B is the area of the base of the prism
H is the height of the prism
we have
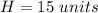
To find the area of the base (hexagon) calculate the area of one equilateral triangle and then multiply by 6
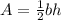
we have
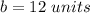
Applying Pythagoras theorem calculate the height of the triangle
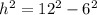
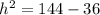
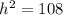
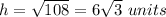
substitute
The area of one triangle is equal to
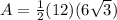
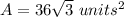
Find the volume of the prism