Question

According to the fundamental theorem of algebra how many roots exist for the polynomial function f(x)=8x^7-x^5+x^3+6

Answer 1

7

Explanation:

This is a 7th degree polynomial. There should be 7 roots. Note how degree of poly = number of roots.

Answer 2

Answer: There are 7 roots for the polynomial function.

Explanation:

Since we have given that

`f(x)=8x^7-x^5+x^3+6`

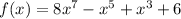
We need to find the number of roots exist for the polynomial.

As we know that

Number of roots = Highest degree of the polynomial.

So, the number of roots = 7

Hence, there are 7 roots for the polynomial function.