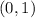ANSWER
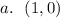
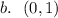
EXPLANATION
a. We want to find the coordinates on the unit circle that corresponds to an angle of 0°
In general, the points on the unit circle are given by,
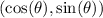
So we substitute,
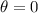
to obtain,
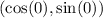
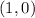
b. For the coordinates of the point on the unit circle that corresponds to an angle of 90º,
We substitute
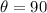
to obtain,
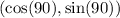
This simplifies to,