Question

A ball is thrown straight up in the air at a velocity

of 100 feet per second. The height of the ball at t seconds
is given by the formula: h = 100t – 5t^2 Find the
maximum height of the ball and when it will land. Maximum Height ____ ft. Land after: ___ seconds

Answer 1

Maximum height = 500 feet

Land after = 20 seconds

Explanation:

Let us follow the movement of the ball as it is thrown upwards. We notice that we get to a point, where the change in the height of the ball with respect to time becomes = 0. This means that the ball is at its maximum position.

Hence, mathematically, at maximum height,
`dh/dt = 0`

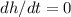
Recall,

`h = 100t - 5t^2`

`dh/dt=100-10t`

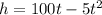
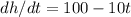
From our problem, we can also deduce that at the maximum height, the velocity of the ball is = 0. i.e
`dh/dt = 0`

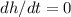
hence,

`0 = 100-10t\\t =10 seconds`

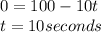
The time the ball takes to reach a maximum height is 10 seconds.

The next step will be to substitute this time value into the equation for the height.

`h = 100(10) -5(10)^2=500 feet`

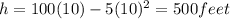
The maximum height is 500 feet

The object will land after t X 2 seconds = 10 X 2 = 20 seconds. This is because it will have to go up and come back down. This should take twice the time.