Question

Find the perimeter of a regular heptagon with consecutive vertices at "A" (-2,-5) and "B" (1,-9)

Answer 1

Perimeter is 35 units.

Explanation:

A heptagon has 7 equal sides.

Given the length of two consecutive vertices, A(-2-5) and B(1,-9).

We can find the length of AB and multiply by 7.

Recall the distance formula;

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

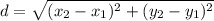
The length of AB is

`|AB|=√((-2-1)^2+(-5--9)^2)`

`|AB|=√((-3)^2+(4)^2)`

`\Rightarrow |AB|=√(9+16)`

`\Rightarrow |AB|=√(25)`

`\Rightarrow |AB|=5\:units`

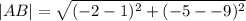
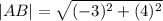
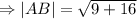
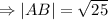
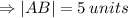
Therefore the perimeter is
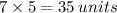`7* 5=35\:units`.