Answer:
1.2%
Explanation:
We are given that the students receive different versions of the math namely A, B, C and D.
So, the probability that a student receives version A =
 .
.
Thus, the probability that the student does not receive version A =
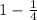 =
=
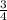 .
.
So, the possibilities that at-least 3 out of 5 students receive version A are,
1) 3 receives version A and 2 does not receive version A
2) 4 receives version A and 1 does not receive version A
3) All 5 students receive version A
Then the probability that at-least 3 out of 5 students receive version A is given by,
 +
+
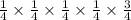 +
+
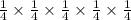
=
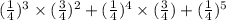
=
![((1)/(4))^3* ((3)/(4))[(3)/(4)+(1)/(4)+((1)/(4))^2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/acbhfpwofn7fney6ic4ufxygc6zkc44vm7.png)
=
![((3)/(4^4))[1+(1)/(16)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/5h88wuje350sc8twyehmdv3e10egh5ekrm.png)
=
![((3)/(256))[(17)/(16)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/4dzffsv6rh0xjlx81ek0fe8v85tb20w2lm.png)
= 0.01171875 × 1.0625
= 0.01245
Thus, the probability that at least 3 out of 5 students receive version A is 0.0124
So, in percent the probability is 0.0124 × 100 = 1.24%
To the nearest tenth, the required probability is 1.2%.