Question

Find the side indicates by the variable. Round to the nearest tenth.

Answer 1

QUESTION 1

The given triangle is right triangle with an acute angle measuring
`53\degree`.

The length of the given side which is opposite to the
`53\degree` angle is 8 units.

Recall that;

`\sin(53\degree)=(Opposite)/(Hypotenuse)`

`\Rightarrow \sin(53\degree)=(8)/(u)`

`\Rightarrow u=(8)/(\sin(53\degree))`

`\Rightarrow u=10.017`

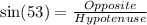
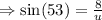
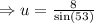
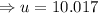
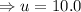`\Rightarrow u=10.0` to the nearest tenth

QUESTION 2

The given right angle triangle has an acute angle measuring
`68\degree`.

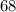The hypotenuse has length 11 units.

`c` is the length of the opposite side.

We use the sine ratio again to obtain;

`\sin(68\degree)=(c)/(11)`

`c=11\sin(68\degree)`

`c=10.197`

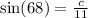
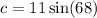
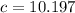
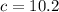`c=10.2` to the nearest tenth.

QUESTION 3

This time the right angle triangle has an acute angle of
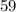`59\degree` and the side opposite this angle is 26 units,

We again use the sine ratio to obtain;

`\sin(59\degree)=(26)/(k)`

`\Rightarrow k=(26)/(\sin(59\degree))`

`\Rightarrow k=30.335`

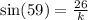
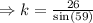
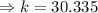
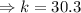`\Rightarrow k=30.3` to the nearest tenth,

QUESTION 4

The given right angle triangle has an acute angle measuring
`22\degree`.

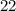The hypotenuse has length 5 units.

`a` is the length of the opposite side.

We use the sine ratio again to obtain;

`\sin(22\degree)=(a)/(5)`

`a=5\sin(22\degree)`

`a=1.875`

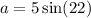
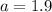`a=1.9` to the nearest tenth.

QUESTION 5

This time the given right angle triangle has an acute angle of
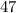`47\degree` and the side opposite this angle has length 51 units.

The side we want to find is adjacent to the given angle. We use the tangent ratio to obtain;

`\tan(47\degree)=(51)/(b)`

`b=(51)/(\tan(47\degree))`

`b=47.558`

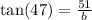
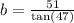
`b=47.6` to the nearest tent.

QUESTION 6

The given right angle triangle has an acute angle measuring
`49\degree`.

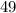The hypotenuse has length 6 units.

The side whose length we want to find is opposite to the given angle, we use the sine ratio to get;

`\sin(49\degree)=(n)/(6)`

`\Rightarrow n=6\sin(49\degree)`

`\Rightarrow n=4.528`

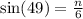
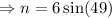
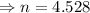
`n=4.5` to the nearest tenth.