QUESTION 1
The given triangle is right triangle with an acute angle measuring
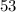 .
.
The length of the given side which is opposite to the
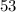 angle is 8 units.
angle is 8 units.
Recall that;
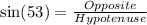
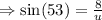
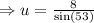
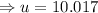
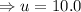 to the nearest tenth
to the nearest tenth
QUESTION 2
The given right angle triangle has an acute angle measuring
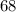 .
.
The hypotenuse has length 11 units.
 is the length of the opposite side.
is the length of the opposite side.
We use the sine ratio again to obtain;
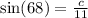
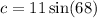
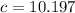
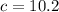 to the nearest tenth.
to the nearest tenth.
QUESTION 3
This time the right angle triangle has an acute angle of
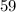 and the side opposite this angle is 26 units,
and the side opposite this angle is 26 units,
We again use the sine ratio to obtain;
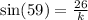
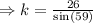
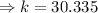
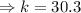 to the nearest tenth,
to the nearest tenth,
QUESTION 4
The given right angle triangle has an acute angle measuring
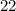 .
.
The hypotenuse has length 5 units.
 is the length of the opposite side.
is the length of the opposite side.
We use the sine ratio again to obtain;
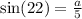
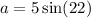
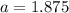
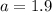 to the nearest tenth.
to the nearest tenth.
QUESTION 5
This time the given right angle triangle has an acute angle of
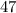 and the side opposite this angle has length 51 units.
and the side opposite this angle has length 51 units.
The side we want to find is adjacent to the given angle. We use the tangent ratio to obtain;
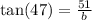
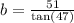
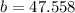
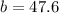 to the nearest tent.
to the nearest tent.
QUESTION 6
The given right angle triangle has an acute angle measuring
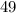 .
.
The hypotenuse has length 6 units.
The side whose length we want to find is opposite to the given angle, we use the sine ratio to get;
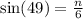
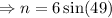
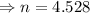
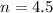 to the nearest tenth.
to the nearest tenth.