Answer:
T(9,-2)
Explanation:
The circle has radius 5 units and center P(6,1).
The equation of this circle is
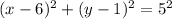
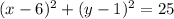
If Q(1,11) lies on this circle, then it must satisfy its equation.
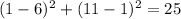
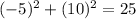
 , this statement is false.
, this statement is false.
If R(2,4) lies on this circle, then it must satisfy its equation.
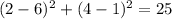
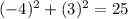
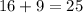 , this statement is false.
, this statement is false.
If S(4,-4) lies on this circle, then it must satisfy its equation.
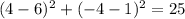
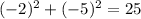
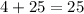 , this statement is false.
, this statement is false.
If T(9,-2) lies on this circle, then it must satisfy its equation.

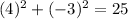
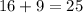 , this statement is TRUE.
, this statement is TRUE.
The correct answer is D