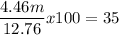Question

An 80-kg rock climber is standing on a cliff so that his gravitational PE =10,000 j. What percent increase in height is required to raise his PE by 3500 j

Answer 1

35.2 %

Step-by-step explanation:

The initial PE of the climber is given by

`PE=mgh`

where

PE = 10,000 J

m = 80 kg is the mass

g = 9.8 m/s^2 is the gravitational acceleration

h = ? is the initial heigth of the climber

Re-arranging the equation, we can find h:

`h=(PE)/(mg)=(10,000 J)/((80 kg)(9.8 m/s^2))=12.8 m`

Now we are told that the PE raises by 3500 J, so we have:

`\Delta PE = mg \Delta h=3500 J`

where
`\Delta h` is the increase in height. Solving for this variable, we find

`\Delta h =(\Delta PE)/(mg)=(3500 J)/((80 kg)(9.8 m/s^2))=4.5 m`

and so, the percent increase in height is

`(\Delta h)/(h) \cdot 100 = (4.5 m)/(12.8 m)\cdot 100=35.2\%`

Answer 2

The answer is:

35 %

Let us solve first the height the rock climber is at, if the gravitational PE=10,000J.

Gravitational PE is the potential energy of an object relative to its position. You can use the formula:

PEgrav = mgh

Where:

PEgrav = gravitational PE

m is mass

g is acceleration due to gravity = 9.8m/s² (this is constant on Earth)

h is height

There is an easy way to do this.

Based on the equation, we know that PEgrav is directly proportional to h. So a percentage increase in height would be equal to the percentage increase in PEgrav and vis-a-vis.

Given that, first we solve the percent increase in PEgrav, by determining what percent is 3,500J of 10,000J.

`(3,500J)/(10,000J)x100=35`

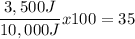
So if there is a 35% increase in PEgrav height, then we can assume that there was a 35% increase in height.

Let's take your problem and solve it the longer way:

Given:

m = 80kg

g = 9.8m/s²

h = ?

PEgrav = 10,000 J

PEgrav = mgh

`10,000J = (80Kg)(9.8m/s^(2))(h)`

`10,000J=(784Kg*m/s^(2))(h)`

`(10,000J)/(784kg.m/s^(2))=h`

`12.76m=h`

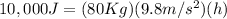
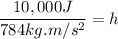
This is the height the rock climber is at given the gravitational PE is 10,000.

Now for the next part, you need to solve for the height to get the PEgrav raised by 3,500J. So the new PEgrav would be 13,500J.

Just do the same procedure again, but instead of 10,000J you will use 13,500J.

`13,500J=(80Kg)(9.8m/s^(2))(h)`

`13,500J=(784Kg*m/s^(2))(h)`

`(13,500J)/(784kg.m/s^(2))=h`

`17.22m=h`

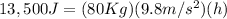
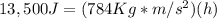
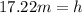
Get the difference between the two heights:

17.22m - 12.76 = 4.46m

Find what percent is 4.46m of the original height:

`(4.46m)/(12.76) x 100=35`