Answer:
C. A horizontal stretch to produce a period of
 and a vertical compression.
and a vertical compression.
Explanation:
We are given the parent function as
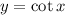
It is given that, transformations are applied to the parent function in order to obtain the function
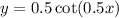 i.e.
i.e.
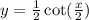
That is, we see that,
The parent function
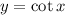 is stretched horizontally by the factor of
is stretched horizontally by the factor of
 which gives the function
which gives the function
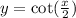 .
.
Further, the function is compressed vertically by the factor of
 which gives the function
which gives the function
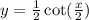 .
.
Now, we know,
If a function f(x) has period P, then the function cf(bx) will have period
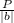 .
.
Since, the period of
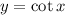 is
is
 , so the period of
, so the period of
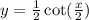 is
is
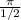 =
=

Hence, we get option C is correct.