Question

Points A(-2, 4), B(1, 3), C(4, -1) and D form a parallelogram. What are the coordinates of D?

A.
(5, 5)
B.
(0, 0)
C.
(1, -2)
D.
(1, 0)
E.
(3, 4)

Answer 1

The answer is D (1,0)

Explanation:

From point B to point A it is left 3 up 1. So from Point C go left 3 up 1 considering it's a parallelogram and there you have it. (1,0)

Answer 2

The coordinates of point D is (1, 0)

Explanation:

Given that points A(-2,4), B(1, 3), C(4, -1) and D form a parallelogram.

we have to find the coordinates of point D.

Let coordinates of point D are (x, y)

By mid-point formula, if (a, b) and (c, d) are the coordinates of two points joining the line segment then the coordinates of mid-point are

`((a+c)/(2), (b+d)/(2))`

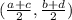
As diagonals of parallelogram bisect each other therefore the mid-point of both diagonals are same.

Mid-point of AC=Mid-point of BD

`((-2+4)/(2), (4-1)/(2))=(1+x)/(2), (3+y)/(2))`

`(1, (3)/(2))=(1+x)/(2), (3+y)/(2))`

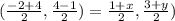
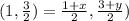
Comparing both sides, we get

`1+x=2` ⇒
`x=1`

`3+y=3` ⇒
`y=0`

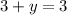The coordinates of point D is (1, 0)

Option D is correct