Question

Two vectors beginning at the same vertex of a triangle are 〈2,3〉 and 〈3,-2〉. Choose the correct classification of the triangle.

Acute
Obtuse
Right
Equilateral

Answer 1

I think maybe a right triangle

I’m sorry if that’s not correct i tried

Answer 2

Right triangle.

Explanation:

The image attached shows those vectors.

Now, assuming that each vector represents each side of the triangle, we can classify it by finding the module of each vector with the following formula.

`l=\sqrt{x^(2) +y^(2) }`

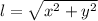
Vector 1.

`l=\sqrt{2^(2) +3^(2) }=√(4+9)=√(13)`

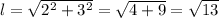
Vector 2.

`l=\sqrt{3^(2) +(-2)^(2) }=√(9+4) =√(13)`

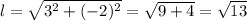
As you can see, the length of each vector (side) is the same, but it's not enough information to it's an equilateral triangle, it could be a right triangle.

Notice that the given points has the same absolute values, but with changes. Specifically, the relation between the given points is

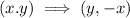`(x.y) \implies (y,-x)`, which is a rotation of 90°.

All this means that those sides are perpendicular to each other, due to the relation of those vectors.

Therefore, the triangle is right, because it has a right angle.