ANSWER
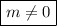
EXPLANATION
The given function is
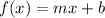
We need to find the inverse of this function,
Let
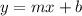
We interchange x an y to obtain,

We solve for y now to obtain,
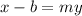
We divide through by m to get,
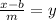
Hence the inverse function is ,

For this inverse to exist, the denominator must not be equal to zero,
Thus
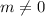
The correct answer is A.