Question

Which statement must be true?

a
b
c
d

Answer 1

Option 1 m≠0 is the right option.

Explanation:

In this question we will find the inverse function first then we will find the gradient of the inverse function to get the correct answer.

The given function is f(x) = mx + b

Or y = mx + b

Now we will rewrite the equation in the form of x.

y - b = mx + b - b

y - b = mx

`x = (1)/(m)y - (b)/(m)`

Now we can write the inverse function as

`f^(-1)(x) = (x)/(m) - (b)/(m)`

Now the gradient of the inverse function is (1/m).Therefor we can easily say that the given function is defined when m≠0 because for m = 0 gradient will be infinity.

Therefore option 1. m≠0 is the right option.

Answer 2

ANSWER


`\boxed {m \\e0}`



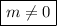
EXPLANATION


The given function is


`f(x) = mx + b`


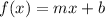
We need to find the inverse of this function,



Let


`y= mx + b`


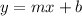
We interchange x an y to obtain,



`x = my + b`


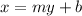
We solve for y now to obtain,



`x - b = my`


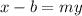
We divide through by m to get,


`(x - b)/(m) = y`


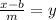
Hence the inverse function is ,



`{f}^( - 1) (x) = (x - b)/(m)`


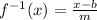
For this inverse to exist, the denominator must not be equal to zero,

Thus


`m \\e0`


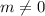
The correct answer is A.